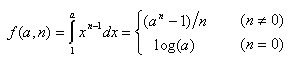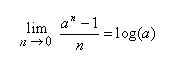Süreklilik

Hayır, süreçlerin sürdürülebilirliği değil, fonksiyonların sürekliliği bugünkü konumuz. Temel derslere geri dönüp bakınca, lisans eğitiminde bazı konuları iyice anlamadan geçtiğimiz ortaya çıkıyor. Süreklilik de böyle bir kavram. İki örnekle anlatmaya çalışacağım.

x^n-1 fonksiyonunun türevi her n için tanımlı. Ama iş türevin tersine gelince, 1/x için belirsiz integral beklenmedik şekilde logaritma çıkıyor. Acaba neden n=0 farklı bir rejim? Bu farklı davranış xⁿ fonksiyonundan türetilebilir mi?

x^n-1 fonksiyonunun 1'den herhangi bir pozitif a sayısına kadar integrali için iki farklı formül var:

f(a, n) n'nin sürekli bir fonksiyonu ise, n parametresi sıfıra yaklaşırken iki ifadenin eşit olması gerekir:

Bu şekilde yazınca hiç de şaşırtıcı değil, çünkü bu ifade, a^x fonksiyonunun x = 0 noktasındaki türevi! Yani xⁿ fonksiyonundan başlayıp a^x fonksiyonunun türevi ile logaritmaya ulaşmış olduk.


İkinci örnek basit bir diferansiyel denklem: y' + y = e^-kt, y(0) = 8
Bu denklemi sağlayan y(t) fonksiyonu için iki ayrı çözüm şekli var:

a) k = 1 ise çözüm üstel fonksiyonun lineer bir ifade ile çarpımı:
y(t) = e^-t (8 + t)

b) k = 1 değilse çözüm iki farklı üstel fonksiyonun toplamı:
y(t) = A e^-t + B e^-kt

Çok farklı iki ifade bulduk ama k parametresi 1'e yaklaşırken iki çözümün yaklaşık eşit olması gerekir. Mesela k = 1.01 için, A ve B katsayıları denklemden ve başlangıç şartından bulunabilir:
y(t) = 108 e^-t − 100 e^-1.01t
Bu ifade şöyle yazılırsa (a) çözümüne yakın olduğu görülür:
y(t) = 8 e^-t + 100 e^-t (1 − e^-0.01t)
Burada e^-0.01t yerine yaklaşık değeri olan 1 − 0.01t koyunca yukarıdaki (a) çözümüne hemen ulaşılır.

Aynı sonuç, e^-xt fonksiyonunun x = 1 noktasındaki türevi olarak da bulunabilir. Yani e^-xt fonksiyonunun t'ye göre türevinden başlayıp aynı fonksiyonun x'e göre türevine ulaşmış olduk.


Meraklı okuyucu için üçüncü bir örnek verelim:
y'' + 2y' + cy = 0, y(0) = 2, y'(0) = 0

a) c=1.00 ise y(t) = 2 e^-t (1 + t)
b) c=0.99 ise y(t) = 11 e^-0.9t − 9 e^-1.1t
c) c=1.01 ise y(t) = 2 e^-t (cos 0.1t + 10 sin 0.1t)

(b) ve (c)deki iki farklı çözüm, c parametresi 1'e yaklaşırken neden (a) çözümüne yaklaşır?

Mezunumuzdan

Böyle bir mektup alınca, 40 senelik eğitim çabalarının meyvesi diyerek seviniyorum.

From: Hande Döngel Altekin
To: Akif Eyler
Date: Feb 18, 2017 at 20:10

Lisans zamaninda pek caliskan oldugumu soyleyemem, fakat simdi Amerikan egitiminin gerektirdigini yapiyorum. Keske 10 sene once bunu anlasaydim, simdi pismanim. Burda 2.30 ortalamaya anormal gozuyle bakiliyor.

Turkiye’de neden oyle oluyor, birbirimizi tembellige mi alistiriyoruz. Gerci ogreniyordum, mantigi aliyordum ama fazla not pesinde kosmuyordum. Turkiyede 85 alinca cok seviniyordum, burda begenmiyorum. Burda farkli olarak yaptigim ve yapmak zorunda oldugum: her hafta dersten once unitenin ozetini cikararak calisiyorum. Cunku herkes oyle yapiyor. Tam gun iste calisip cocuklari olmasina ragmen bir de derse calisip geliyorlar. Hoca da calisilmis olarak varsayip detaylari vererek, mantigini pekistiyor, ders sonunda quiz yapiyor veya bir case isleniyor. Calisip gitmek gerekiyor. Yoksa anlamiyorsun. Gecen donem bir hocanin dersinde quizler sayesinde bu tempoya alistim bu donem o yuzden rahat ediyorum. Ayiptir soylemesi 4.00 ortalama yaptım.

Genc arkadaslar "ben zaten master yapmayacagim ortalama bana gerekli degil" demesinler. Annem demisti; "benim zamanimda lise mezunu olmak yeterdi. Universite okumak ekstra gibi gozukurdu. Simdi normal olan universite mezunu olmak, ben geride kaldim. O yuzden sen master yapmalisin. Ileride gerekecek” Ben dinlememistim ilk mezun oldugumda ama master artik sart, 30 yasinda mastera basladim.

Hande'nin yazdıkları beni uzun uzun düşündürdü. Farklı okullarda yıllardır verdiğim Automata ve Simulation derslerini Amerika'daki benzeri derslerle kıyasladım. Aynı kitapları okutuyoruz, aynı programı izliyoruz ama sonuç aynı olmuyor. Neden? Çünkü aynı ağırlıkta ödevler veremiyoruz, benzer zorlukta sınavlar yapamıyoruz. Bir dönemde 3-4 ödev bile çok geliyor buradaki öğrenciye. Sınav derseniz, derste anlattığımız konuyu bile sınavda geri alamazken, her sınavda orijinal, kitap dışı soruları kime, nasıl soracağız?

Örnek olarak, MIT'deki Automata dersinin 2006 sınavları ile FSMVÜ'de aynı dersin 2016 sınavını kıyaslayabilirsiniz. Bu nedenle iki taraftaki eğitimin kalitesi aynı olamıyor. Çalışma alışkanlıkları çok farklı.

Alim okulu -- AFL

Tam 50 sene önce (28 Ekim 1964) bir haber

"Ankara'da âlim yetiştirecek bir okul açıldı"

Bu gazeteyi görmedim ama bundan üç yıl sonra, Ankara Fen Lisesi ilk mezunlarını verdiği sene, kendimi orada birinci sınıfta buldum. Babam bir taksiyle beni dağın başında bir yere götürüp bıraktı. Dönüşte taksi sürücüsü sormuş: "Kusura bakma Abi, çocuğu neden bıraktın?" Okumak için bıraktığını, hem de İstanbul'dan geldiğini duyunca: "Abi, orada hiç okul bulamadın mı da buralara getirdin?"

AFL 1964 -- Derslikler ve idare binası
Issız bir dağ başında yatılı okul

Böyle bir okul hakikaten başka yerde yoktu. 24 kişilik sınıflarda, seçme öğretmenlerin gözetiminde, başka liselerde hayal bile edilemeyen laboratuvar ve kütüphane imkanlarına sahip olduk. Matematik derslerinde düşünmeyi öne alan "modern müfredatı" takip ederken, fen derslerinin her birinde haftada bir deney yapıyorduk.

İlk iki yıl sorunsuz geçti ama son sınıfta bizi bir düşünce aldı: Üniversite seçme sınavında ne yapacaktık? Sınavda klasik müfredata uygun sorular sorulduğu için, önceki mezunlar pek başarılı olamıyor, ancak özel sınavla alan okullara girebiliyordu. Yönetim "sizin için uğraşıyoruz" diyordu ama dağın başındaki 90 çocuk kimin umurunda?

Sınava girince sürprizi gördük: Fen soruları iki grupta toplanmış. 72 soru klasik, 72 soru modern müfredata göre. En başında yazıyor: "Okuduğunuz müfredata uyan soruları çözün." O anda bir tahmin yaptım: İki gruptaki soruların cevabı aynı şık olmalı. Yani 13. sorunun klasik cevabı C ise modern cevabı da C'dir. Bu bize büyük avantaj sağladı, 90 kişiden üçü ilk beş arasına girdi.

Yazının ayrıntılarından çok, resimde görülen genç öğretmenden söz etmem lazım: Faruk Aysu biyoloji anlatırdı. İşini bu kadar severek yapan kişi her meslekte az bulunur. Faysu tam bir idealistti, birkaç olayda söylediği "Allah'tan başka kimseden korkmam" sözünü hâlâ unutmuyorum. Bizden sonra uzun süre okul müdürü olarak görev yaptı. 

İlk gördüğümde dağ başında olan AFL, son gittiğimde mahallelerin arasında kalmış. 

File-Edit-View

Otuz sene önceydi. 1984'de ilk Macintosh çıktığında GUI diye bir şey duyduk. Fare, pencere, menü... hepsi ilk Mac üstünde gördüğümüz yepyeni kavramlardı. Sol üst köşede küçük bir siyah elma ve yanında değişmeyen üç kelime: File-Edit-View.

Mac ile birlikte gelen bir kavram da localization -- yerelleştirme. O zamanlar Komili'nin olan Bilkom, yerelleştirme konusunda Boğaziçi Üniversitesinde bize danıştığında, bu menüler "Dosyalama-Düzenleme-Görüntüleme" olarak tercüme edilmişti. "Dosya-Düzen-Görüntü" halini alması için epeyce uğraşmamız gerekti. :)

Yıllar sonra Mac yazılımı çok değişti ama bu üç kelime aynen duruyor:

Bugün yaptığım bir arama, File-Edit-View menü üçlüsünün ilk olarak 2005'de tarayıcılardan kaldırıldığını gösteriyor. Bazılarımız bu özellikten vazgeçmedi, Firefox'da klasik menüleri görmeden yapamıyorum.

Otuz yıldır değişmeyen bir başka GUI özelliği ise Double-click -- çift tıklama. O zamanlar bunun geçerli bir mantığı vardı: Önce seç, sonra emret. "Bir dosya üstünde işlem yapmak için, önce fare ile dosyayı seçin, sonra menüden gerekli komutu bildirin." En sık kullanılan komut "Aç" olduğundan, çift tıklama bu işlemin kısa yolu olarak tanımlanmıştı.

Donanımın hızlanması ve yazılımın gelişmesi ile, dosya seçmek için tıklamaya gerek olmadığı anlaşıldı! Dosyanın üstüne gitmek, seçmek için yeterliydi, tıklamaya gerek yoktu. On yıl geçmesi ve ilk web tarayıcılarının ortaya çıkması gerekti. Şimdi yirmi yıl daha geçti. Web sayfalarında tek tıklama yeterli iken, dosya açmak için hâlâ çift tıklama standart davranış olarak duruyor.

Bir origami eserinin doğuşu

Malzeme çok basit ve ucuz: Renkli fotokopi kağıdı. Kesmek için makas kullanmam. Uzun kesitler için giyotin uygun -- makas hiçbir elde bu kadar düzgün kesemez. Parçaları birbirinden ayırmak için mektup açacağı yeterli.

Bu örnek için seçtiğim 12-yüzlü (dodecahedron) beş renkten altışar adet modül ile yapılıyor. Katlama yöntemi burada.

30 adet modül kesildi ve katlandı, kontrast oluşturan renkler üstünde poz veriyorlar.  Ortaya çıkacak şekil henüz ancak yapımcının aklında.

Her renkten ikişer parça kullanınca ayaklı bir beşgen ortaya çıktı.

Parçaların üçte ikisi yerini aldı -- on iki yüzün altısı tamam.
Her yüzde (ve her kenarda) beş rengin herbiri var.

İşte beş renkli onikiyüzlümüz hazır. Yıllar önce dünyaya gelen altı renkli ablasının yanına ne güzel yakıştı :)

Origami güzeldir, insanı ferahlatır, mutluluk verir:
Bir iş bitirmenin mutluluğu...

Origami Mutluluk Verir

Origami merakı, fakültedeki uzun toplantıların bir yan ürünü olarak 15 yıl önce ortaya çıkmıştı. Bir süre uzak kaldıktan sonra, 2012'de CAS161 dersini tekrar açtım. İlgi gördüğü sürece, bu dersi yine vermek isterim.

2012 Sergisinden bir kesit

2013 Sergisindeki işlerden bir kısmı

Daha sonra Üsküdar Çocuk Üniversitesi karşıma çıktı. Şubat'ta haftada bir gitmeye başladım. Üç ay geçti, çocuklar da ben de çok şey öğrendik. Mesela, daha önce düz beyaz kağıt kullanırdım, çocukların ilgisini çeksin diye artık renkli çalışıyoruz.

Üsküdar Çocuk Üniversitesinde yaptığımız işler

Bu çocuklar neden böyle mutlu oluyor? Çünkü daha önce görmedikleri geometrik bir cismi, biraz tarif, çokça sabır, biraz da yardımla bir saat içinde yapabiliyorlar. Çok basit malzeme ile bir şeyler üretebilmenin mutluluğu bu olsa gerek... Dün yaptığımız beş renkli onikiyüzlü, bir sonraki yazının konusu olsun.

Üç renk = Üç boyut

Origaminin bana verdiği mutluluk ise geometrik modellerin kısa sürede yapılması ve simetri yapısının gösterilmesi. Bu çalışmada, küb ile düali, küboktahedron ile düali aynı eksenlere oturmuş. Her cisimde sarı-yeşil-mavi üçgeninden sekiz tane var. Bu güzelliği başka bir yöntemle bu kadar hızlı gösterebilir misiniz?